重力加速度により雨滴の速度は増し続けるように思えますが、実際にはある値に落ち着きます。そのメカニズムを解説します。
1. 微分方程式
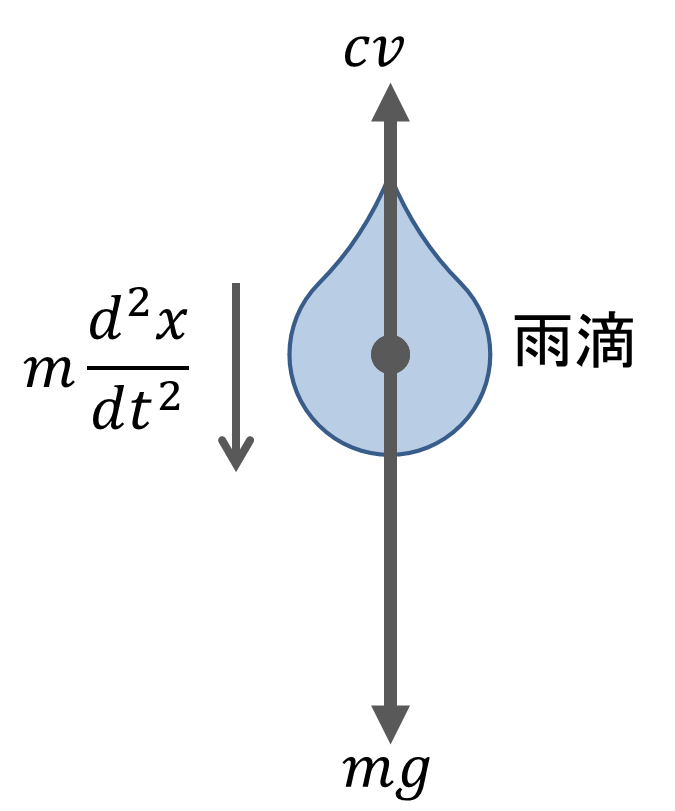
大気中の小さな雨滴(質量\(m\))に働く力は、鉛直下向きの重力\(mg\)と鉛直上向きの粘性抵抗(空気抵抗)\(cv\)です。したがって、鉛直下向きを\(+x方向\)とすると、雨滴の運動方程式は
\[m\frac{\displaystyle d^2 x}{\displaystyle dt^2}=m\frac{\displaystyle dv}{\displaystyle dt}=mg-cv ・・・(1)\]
となります(\(v=dx/dt\))。
落下しはじめは落下速度\(v\)が小さいので粘性抵抗は無視でき、雨滴は重力加速度\(g\)の等加速度直線運動をします。雨滴の速さ\(v\)が増加するのにつれて粘性抵抗が増加するので、雨滴に働く下向きの合力の大きさは減少し、したがって加速度も減少していきます。速さ\(v\)が
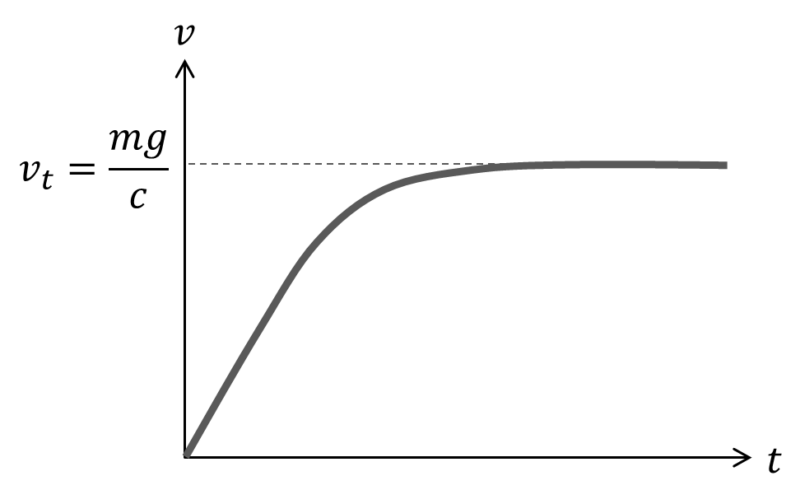
\[v=v_t \equiv \frac{\displaystyle mg}{\displaystyle c} ・・・(2)\]
になると雨滴に働く力は0になるので、雨滴は速さ\(v_t\)の等速落下運動をするようになります。この速さ\(v_t\)を終端速度といいます。
2. 微分方程式を解く
微分方程式
\[m\frac{\displaystyle dv}{\displaystyle dt}=mg-cv ・・・(1)\]
を解いてみたいと思います。この式の右辺には\(v\)が含まれているので、この式の両辺を\(t\)で積分して求めることはできません。そこで、\(dv/dt\)は\(\delta v \div \delta t\)の\(\delta t→0\)の極値なので、\(dv/dt=\delta v \div \delta t\)とみなして式(1)を
\[m \, dv=(mg-cv)dt\]
したがって
\[\frac{\displaystyle dv}{\displaystyle mg/c-v}=\frac{\displaystyle c}{\displaystyle m}dt ・・・(3)\]
と変形します。式(3)の右辺には\(v\)だけが現れ、右辺に\(t\)だけが現れるので、左辺を\(v\)について積分し、右辺を\(t\)について積分すると
\[\int\frac{\displaystyle dv}{\displaystyle mg/c-v}=\int \frac{\displaystyle c}{\displaystyle m}dt ・・・(4)\]
となります。\(1/(A-v)\)の原始関数は\(-log |A-v|\)なので式(4)は
\[-log \left| \frac{\displaystyle mg}{\displaystyle c}-v \right|=\frac{\displaystyle ct}{\displaystyle m}+K(Kは任意定数)\]
となります。ここで\(log\)は\(e\)を底とする自然対数を意味します。時刻\(t=0\)に落下し始めるので\(v(t=0)=0\)となります。したがって
\[K=-log \left( \frac{\displaystyle mg}{\displaystyle c} \right) ・・・(5)\]
となります。\(A=e^B\)と\(B=log \,A\)は同じ関係を表すので、
\[\begin {eqnarray}
\frac{\displaystyle ct}{\displaystyle m} &=&
-log \left| \frac{\displaystyle mg}{\displaystyle c}-v \right|-K = -log \left( \frac{\displaystyle mg}{\displaystyle c}-v \right)+log\frac{\displaystyle mg}{\displaystyle c} \\
&=& log\frac{\displaystyle mg/c}{\displaystyle mg/c-v} ・・・(6)\end {eqnarray}\]
この式は
\[\frac{\displaystyle mg/c}{\displaystyle mg/c-v}=e^{ct/m}\]
したがって
\[v=\frac{\displaystyle dx}{\displaystyle dt}=\frac{\displaystyle mg}{\displaystyle c}(1-e^{ct/m}) ・・・(7)\]
となります。
物体が粘性抵抗などの抵抗力を受けて運動する場合には、位置エネルギーは減少するのに運動エネルギーはそれと同じだけは増加しません。なぜなら、力学的エネルギーが減少している分は熱エネルギーになっているためです。
雨滴の時間\(t\)での落下距離\(x(t)\)は式(7)の\(x(t=0)=0\)の解なので
\[x(t)=\frac{\displaystyle mg}{\displaystyle c}t-\frac{\displaystyle m^2g}{\displaystyle c^2}(1-e^{-ct/m}) ・・・(8)\]
