運動の法則の2次元運動への応用例として斜方投射による放物運動を解説します。
1. 放物運動
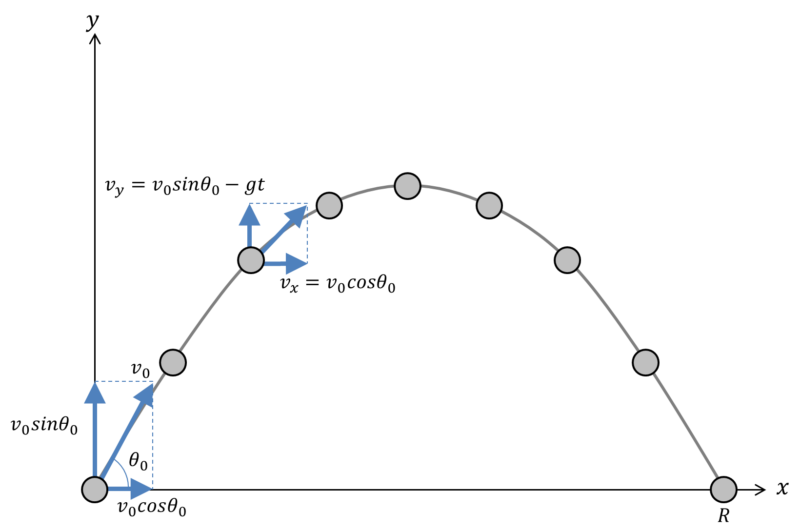
水平な地面の上で物体を空中に斜めに投げる場合を考えます。この運動は、空気の抵抗が無視できる場合には、水平方向の等速運動と鉛直上方への投げ上げ運動を重ね合わせた運動です。投げる向きの水平方向を\(+x\)方向、鉛直上向きを\(+y\)方向、初速度\(v_0\)が水平となす角を\(\theta_0\)とすると、初速度の水平方向成分(\(x\)成分)は\(v_0\)が水平となす角を\(\theta_0\)とすると、初速度の水平方向成分(\(x\)成分)は\(v_{0x}=v_0cos\theta_0\)となります。
水平方向(\(x\)方向)の運動は、加速度が\(a_x=0\)なので、速さ\(v_x\)が初速\(v_{0x}=v_0cos\theta_0\)の等速運動、
\[v_x=v_{0x}=v_0cos\theta_0 ・・・(1)\]
となります。したがって、投げてからの時間が\(t\)のときの水平方向の移動距離\(x\)は
\[x=v_{0x}t=(v_0cos\theta_0)t ・・・(2)\]
物体の速度の鉛直方向成分(\(y\)成分)\(v_y\)は、放り投げたときの値\(v_{0y}=v_0sin\theta_0\)から下向きの重力加速度\(-g\)で減少していきます。したがって、
\[v_y=v_{0y}-gt=v_0sin\theta_0-gt ・・・(3)\]
となります。物体が手を離れてから時間\(t\)経過したときの高さ\(y\)は式(3)を時間で積分して
\[y=v_{0y}t-\frac{\displaystyle 1}{\displaystyle 2}gt^2=(v_0sin\theta_0)t-\frac{\displaystyle 1}{\displaystyle 2}gt^2 ・・・(4)\]
となります。
最高点では物体の速度の\(y\)成分は\(0\)(\(v_y=0\))なので、物体が最高点に到達するまでの時間\(t_1\)は、\(v_y=v_{0y}-gt_1=v_0sin\theta_0-gt_1=0\)から、
\[t_1=\frac{\displaystyle v_{0y}}{\displaystyle g}=\frac{\displaystyle v_0sin\theta_0}{\displaystyle g} ・・・(5)\]
となります。最高点の高さ\(H\)は式(5)を式(4)に代入すると得られます。
\[H=\frac{\displaystyle {v_{0y}}^2}{\displaystyle 2g}=\frac{\displaystyle (v_0sin\theta_0)^2}{\displaystyle 2g} ・・・(6)\]
次に、物体の軌道を求めるために式(2)から導かれる
\[t=\frac{\displaystyle x}{\displaystyle v_{0x}}=\frac{\displaystyle x}{\displaystyle v_0cos\theta_0} ・・・(7)\]
を式(4)に代入すると
\[y=\frac{\displaystyle v_{0y}}{\displaystyle v_{0x}}x-\frac{\displaystyle g}{\displaystyle 2{v_{0x}}^2}x^2=\frac{\displaystyle sin\theta_0}{\displaystyle cos\theta_0}x-\frac{\displaystyle g}{\displaystyle 2(v_0cos\theta_0)^2}x^2 ・・・(8)\]
が導かれます。

これが物体の放物運動の軌道の放物線を表します。
式(8)の第2辺の第1項
\[y=\frac{\displaystyle v_{0y}}{\displaystyle v_{0x}}x すなわち \frac{\displaystyle y}{\displaystyle x}=\frac{\displaystyle v_{0y}}{\displaystyle v_{0x}}=\frac{\displaystyle sin\theta_0}{\displaystyle cos\theta_0} ・・・(9)\]
は初速度\(v_0\)の方向の等速直線運動の軌道を表します。第2項の
\[y=-\frac{\displaystyle g}{\displaystyle 2{v_{0x}}^2}x^2 ・・・(10)\]
は初速\(v_{0x}\)の水平方向への投射運動の軌道を表します。

水平投射運動での落下距離は自由落下運動での落下距離に等しいので、放物運動は等速直線運動と自由落下運動の2つの運動の重ね合わせになります。
2. モンキーハンティング
モンキーハンティングという思考実験があります。気の枝にぶら下がっている猿に照準を合わせて弾丸を発射するのと同時に、それを見た猿が枝から手を離すと弾丸は猿に命中するという、動物虐待にあたる困った思考実験です。そこで、今回は猿を単に物体に置き換えたいと思います。
物体が地面に落下する地点までの距離\(R\)は、軌道の式(8)で物体の高さ\(y\)が\(0\)になるときの\(x\)の値として求められます。\(y=0\)とおくと
\[\frac{\displaystyle sin\theta_0}{\displaystyle cos\theta_0}x-\frac{\displaystyle g}{\displaystyle 2(v_0 cos\theta_0)}-\frac{\displaystyle g}{\displaystyle 2(v_0cos\theta_0)^2}x^2=\frac{\displaystyle x(2{v_0}^2sin\theta_0cos\theta_0-gx)}{\displaystyle 2(v_0cos\theta_0)^2}=0 ・・・(11)\]
となります。この式の解は2つありますが、そのうち\(x=0\)という解は投げた点なので、求める距離\(R\)はもう1つの解に対応します。
\[R=\frac{\displaystyle 2{v_0}^2sin\theta_0cos\theta_0}{\displaystyle g}=\frac{\displaystyle {v_0}^2 sin2\theta_0}{\displaystyle g}・・・(12)\]
となります。ここで\(2sin\theta_0cos\theta_0=sin2\theta_0\)という関係式を使いました。
