ねじ山に働く摩擦力のモデル化と関係式を導出します。
モデル
ねじの摩擦を考える上で、次のような展開図を想像してください。ねじの有効径を\(d\)、ピッチを\(p\)としています。ねじにを締めこむことで発生する「軸力\(Q\)で発生する摩擦力\(F\)」に逆らって\(P\)の力で締めこまなければなりません。
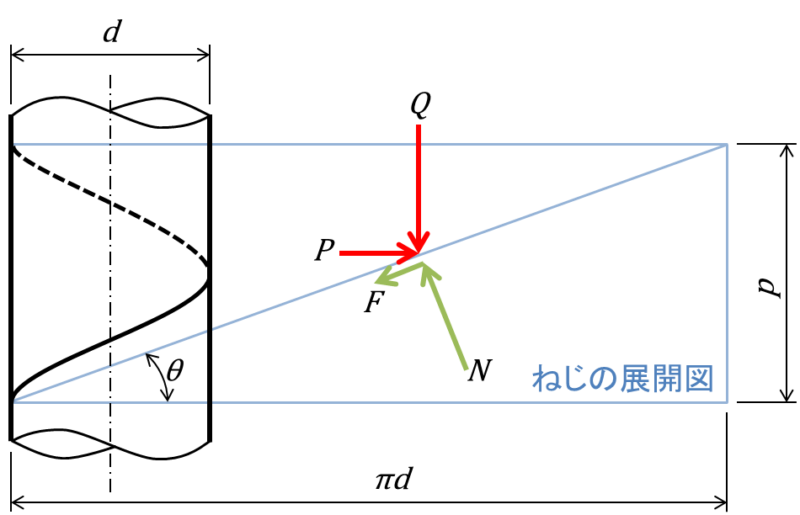
定式化
傾きの角度は次のように表されます。
\[
tan \theta = \frac{\displaystyle \theta}{\displaystyle \pi d} ・・・(1)
\]
力のつり合いから\(P\)、\(Q\)は次のように定義できます。
\[
P=N \, sin\theta+F\, con \theta ・・・(2)
\\
Q=N \, cos \theta-F\, sin \theta ・・・(3)
\]
ここで、摩擦力\(F\)と垂直抗力\(N\)の関係に対して、摩擦係数\(\mu=tan\alpha \)と置くと次のように表されます。
\[
F=N\, \mu =N\,tan\alpha ・・・(4)
\]
式(2)~(4)より
\[
P=Q\frac{\displaystyle sin\theta+tan\alpha\, cos\theta}{\displaystyle cos\theta-tan\alpha\, sin\theta } = Q tan(\theta+\alpha) ・・・(5)
\]
となります。ここで式(1)を用いると次の式が得られます。
\[
tan(\theta+\alpha)=\frac{\displaystyle tan\theta+tan\alpha}{\displaystyle 1-tan\theta\,tan\alpha}=\frac{\displaystyle p+\mu\pi d}{\displaystyle \pi d- \mu p} ・・・(6)
\]
ねじを回すために必要なトルクは次のように導出できます。
\[
T=Pd/2=\frac{\displaystyle 1}{\displaystyle 2}Qd\,tan(\theta+\alpha)=\frac{\displaystyle 1}{\displaystyle 2}Qd\frac{\displaystyle p+\mu \pi d}{\displaystyle \pi d – \mu p} ・・・(7)
\]
なお、ねじが緩まないための条件は「\(\theta<\alpha\)」=「\(p<\mu \pi d\)」となります。
