ゼロから分かるアルキメデスの原理｜浮力が働くメカニズム

　アルキメデスの原理を図と物理法則を基にわかりやすく解説します。

1. 浮力のモデルと物理式

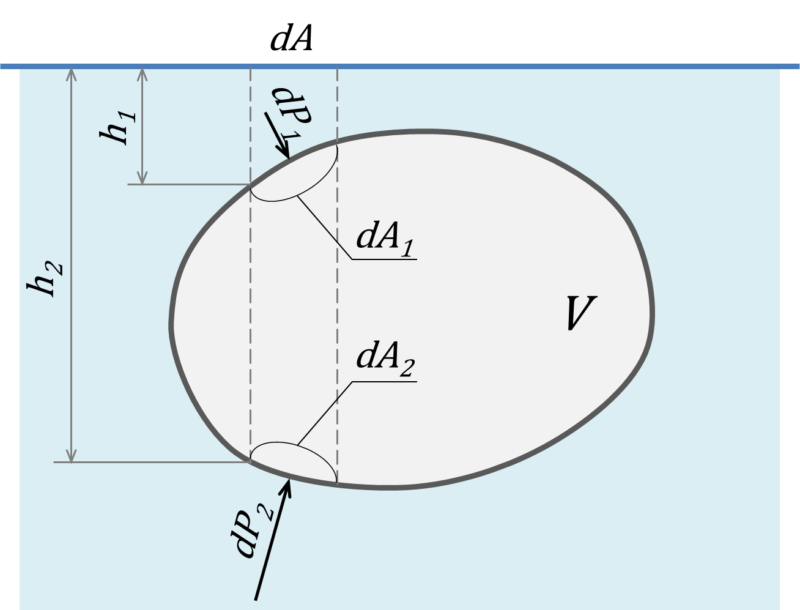
　流体中に物体が置かれると、その表面には圧力が作用します。図の様に体積\(V\)を微小断面積\(dA\)で物体を区分けして考えます。上面、下面の表面積を\(dA_1、dA_2\)とし、水面からの深さを\(h_1、h_2\)とします。すると、上面、下面に働く圧力によって発生する力は次のようになります。
\[
dP_1=\rho g h_1 dA_1 \\
dP_2=\rho g h_2 dA_2
\]
ここで、\(\rho g h\)はそれぞれの水深\(h\)における水圧を表しており\(水圧\times 面積=力\)という構図になります。

この力の鉛直方向（重力に沿った方向；上下方向）の成分は次のようになります。
\[
dP_{10}=\rho g h_1 dA \\
dP_{20}=\rho g h_2 dA
\]

したがって、物体の上面と下面に働く圧力の差は次のようになります。
\[
F=\int_V (dP_{20}-dP_{10})=\rho g \int_V (h_2-h_1) dA=\rho g V
\]

この力\(F\)が浮力となります。この式から浮力は物体が押しのけた体積\(V\)の液体の重さに等しいことがわかります。これをアルキメデスの原理といいます。

2. 船が転ばずに安定して浮ける理由

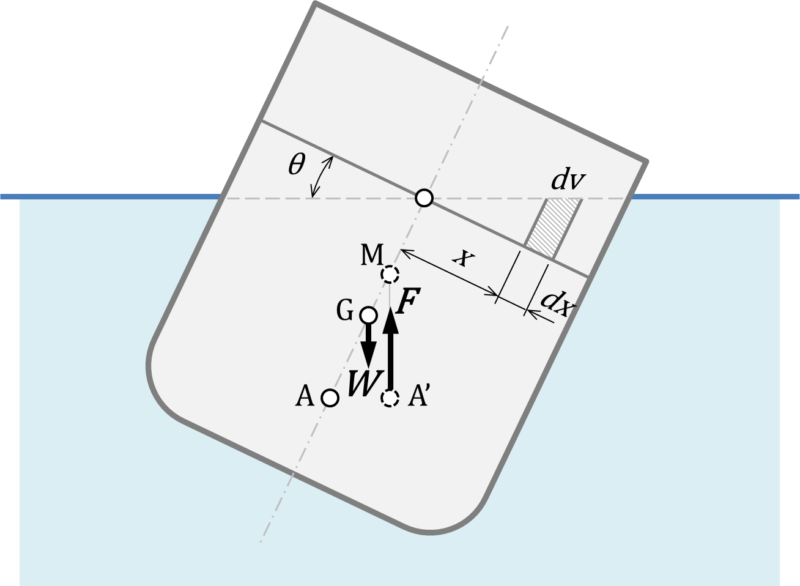
　図の様に、水面に浮かんでいる物体が押しのけた水の体積を\(V\)、重量\(W\)が重心\(G\)に作用しており、浮力\(F\)の作用点を\(A\)とします。

物体が\(\theta\)傾いた場合の安定性について考えます。このとき、浮力の作用点が\(C\)が\(C’\)に移り、その場合の浮力と元の中心線との交点を\(M\)とします。

傾くことによって新たに水中に貼ることによって生じた浮力\(\rho g V\)によるモーメントは、微小容積\(dV=x tan(\theta) dx\)であることを利用して次のように表されます。
\[
dM=\rho g dVx =\rho g tan(\theta) x^2 dx
\]

逆に、反対側は水面上に出る事で浮力を失うため、これを総合して物体が傾いたことにより獲得・消失した浮力により生じるモーメントは次のようになります。
\[
M=2\int \rho g dV x =2\rho g tan(\theta)
\]

ここで、液面の平面上の軸に関する慣性モーメント\(I\)と置くと\(2\int x^2 dx = I\)であることから
\[M=\rho g tan(\theta)I\]
となります。

ここで、\(M\)が\(G\)の上にあれば安定であり、逆に\(M\)が\(G\)の下にあれば不安定となります。したがって、この\(\overline{GM}\)の大きさは安定度を示しています。この\(M\)点をメタセンターといいます。