
流体力学を学ぶ上で一つのハードルであるナビエ・ストークスの方程式を、基礎を振り返りつつ導出の過程を解説します。
1. 粘性
流体はその変形に際して抵抗を受けます。この関係は変形速度とせん断応力の関係で表わすことができます。最も単純な場合として、下図の様に平行平板間に粘性流体を満たし、下面の板を固定し、上面の板を一定速度で移動させた時の流れを考えます。
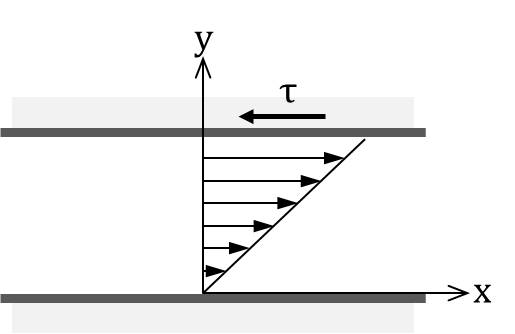
下面に働くせん断応力\(\tau\)は、
\[\tau=\mu\left( \frac{\displaystyle du}{\displaystyle dy} \right)_{y=0} ・・・(1)\]
ここで、
\[\mu:粘性係数 [Pa\cdot sec]\]
式(1)に従う流体をニュートン流体、式(1)に従わない流体を非ニュートン流体とよびます。一般の流体力学ではニュートン流体のみを取り扱います。非ニュートン流体についてはレオロジー(rheology、物質の変化と流動に関する科学)の分野で扱われます。

私たちの生活圏に存在する空気や水をはじめとする天然の流体は全てニュートン流体として近似できます。
2. オイラーの運動方程式
先ず、粘性を取り扱うナビエ・ストークスに入る前に、非粘性を取り扱うオイラーの運動方程式について解説します。次の記事では運動方程式(流体の運動量保存則)の物理的な意味を高校物理のレベルで解説しましたので、まずはそちらをご覧ください。ここでは3次元に拡張して考えていきたいと思います。
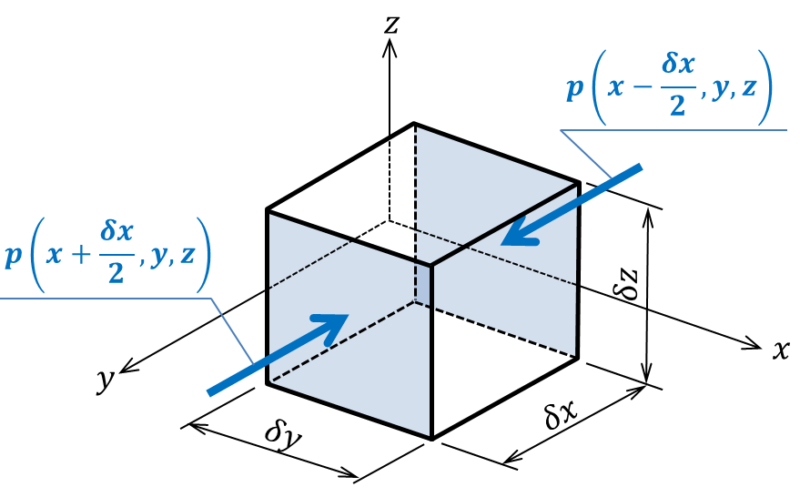
先ず、上図のような微小流体塊を考えます。※ここで()は演算ではなく座標を表します
完全流体中に働く力は質量力(重力、浮力、コリオリ力など)と圧力のみです。
(1)微小流体塊に働く”圧力”
x軸に垂直な面に働く圧力差を考えると
\[
\left\{
p \left(x-\frac{\delta x}{2},y,z \right)-p_\left(x+\frac{\delta x}{2},y,z \right) \right\}
\delta y \delta z
・・・(2)\]
上式をテイラー展開すると
\[
\left\{ p_{x,y,z,t}+\frac{\partial p}{\partial x}\left( -\frac{\delta x}{2}\right)\right\}\delta y \delta z
-\left\{ p_{x,y,z,t}+\frac{\partial p}{\partial x}\left( \frac{\delta x}{2}\right)\right\}\delta y \delta z
+ \left\{O\left((\delta x)^2\right)\right\}\delta y \delta z ・・・(3)
\]
ここで\(O\)は高次の次数(hight order)を表しており、これを0と近似すると上式は
\[-\frac{\partial p}{\partial x}\delta x \delta y \delta z ・・・(4)\]
同様にy軸に垂直な面、z軸に垂直な面を考えると
\[-\frac{\partial p}{\partial y}\delta x \delta y \delta z ・・・(5)\]
\[-\frac{\partial p}{\partial z}\delta x \delta y \delta z ・・・(6)\]

ここで\(\delta x \delta y\)は面積を表すので、「面積×圧力p」の形になり、”力”を表すんですね。
(2)微小流体塊に働く”質量力”
単位質量あたりに働く外力を\(\bf{F}\it(F_x,F_y,F_z)\)とすると質量力は
\[\rho\bf{F}\it \delta x \delta y \delta z=\rho
\left[\begin{matrix} F_x\\F_y\\F_z \end{matrix}\right]\delta x \delta y \delta z ・・・(7)\]

ここで\(\delta x \delta y \delta z\)は体積を表すので、「体積×密度ρ」は”質量”を表すんですね。
(3)ニュートンの第2法則による運動量保存式
ニュートンの第2法則\(m \bf{a}=\bf{F}\)より、

・・・(8)
ここで、
\(\bf{U}\it=(u,v,w)\):流速
\(\frac{D}{Dt}=\frac{\partial }{\partial t}+ u\frac{\partial }{\partial x}+ v\frac{\partial }{\partial y}+ w\frac{\partial }{\partial z} \):実質微分(オイラー微分)
上式をx成分について表すと次のようになります。
\[\frac{Du}{Dt}=F_x -\frac{1}{\rho}\frac{\partial p}{\partial x} ・・・(9)\]
ニュートンの第1法則:慣性の法則
ニュートンの第3法則:作用、反作用
3. 応力テンソル(粘性流体について)
粘性流体の場合、微小流体塊には次の図のような応力が働きます。
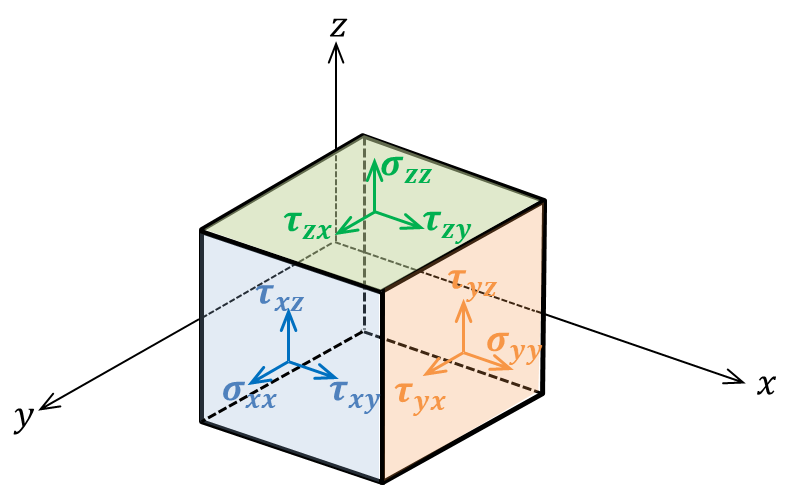
応力は温度などのスカラー量、流速のようなベクトル量とは異なり、次のようなテンソル量で表わされます。
\[P=\left[\begin{matrix}
\sigma_{xx}&\tau_{yx}&\tau_{zx}
\\ \tau_{xy}&\sigma_{yy}&\tau_{zy}
\\ \tau_{xz}&\tau_{yz}&\sigma_{zz}
\end{matrix}\right] ・・・(10)\]
ここで、\(\sigma_{\alpha\beta}\):法線応力、\(\tau_{\alpha\beta}\):せん断応力です。添え字の\(\alpha\)は考えている面の方向を、\(\beta\)は力の成分方向を示します。
応力テンソルは対角成分が等しい対角テンソルであるため、
\[\tau_{xy}=\tau_{yx}, \tau_{yz}=\tau_{zy}, \tau_{zx}=\tau_{xz} ・・・(11)\]
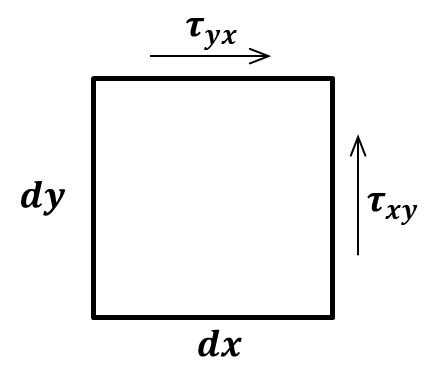
このことは、微小流体のある一点のまわりに働く回転モーメントを考えれば容易にわかります。
\[\tau_{xy}dx-\tau_{yx}dy+(体積力のモーメント)=0\]
微小流体の体積をゼロの極限にすると、体積力(質量力と慣性力)のモーメントは表面力のモーメントに比べて高次の無限小であり無視できます。それゆえ、表面応力の回転モーメントのつり合い条件から式(11)が得られます。

流体中の応力は流体の相対運動の結果として生じるので、式(10)に定義した応力テンソルは流体運動と関連付けなければなりません。この関係を一般的に導くのは厄介なので、ここでは類推による説明で感覚的に理解を深めたいと思います。
ある流れ場の中に立方体を考えます。次の図(a)の様に、立方体の面と流線の方向は必ずしも一致しておらず、流線は各方向成分に分解されます。
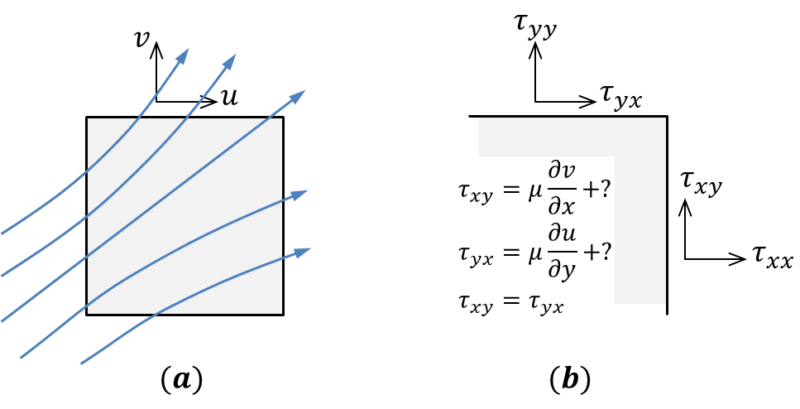
図(b)の様に、隣り合うx面とy面とのせん断応力を考えると、y面の\(\tau_{yx}\)は式(1)で示した様に\(\mu\frac{\partial u}{\partial y}\)の項を含み、\(\tau_{xy}\)は\(\mu\frac{\partial v}{\partial x}\)の項を含まなければならないため、せん断応力は次式の様に表されます。
\[ \begin{cases}
\tau_{xy}=\tau_{yx}=\mu\left( \frac{\displaystyle\partial v}{\displaystyle\partial x}+\frac{\displaystyle\partial u}{\displaystyle\partial y} \right)
\\
\tau_{xz}=\tau_{zy}=\mu\left( \frac{\displaystyle\partial w}{\displaystyle\partial y}+\frac{\displaystyle\partial v}{\displaystyle\partial z} \right)
\\
\tau_{zx}=\tau_{xz}=\mu\left( \frac{\displaystyle\partial u}{\displaystyle\partial z}+\frac{\displaystyle\partial w}{\displaystyle\partial x} \right)
\end{cases} ・・・(12)\]
一方で法線応力は式(12)と同様に考えると\(2\mu\frac{\partial u}{\partial x}\)の項を持ち、これに圧力\(p\)と圧縮性によるみずみ応力を考慮すると、
\[ \begin{cases}
\sigma_{xx}=-p -\frac{\displaystyle 2}{\displaystyle 3}\mu \Theta+2\mu\frac{\displaystyle\partial u}{\displaystyle\partial x}
\\
\sigma_{yy}=-p -\frac{\displaystyle 2}{\displaystyle 3}\mu \Theta+2\mu\frac{\displaystyle\partial v}{\displaystyle\partial y}
\\
\sigma_{zz}=-p -\frac{\displaystyle 2}{\displaystyle 3}\mu \Theta+2\mu\frac{\displaystyle\partial w}{\displaystyle\partial z}
\end{cases} ・・・(13)\]
ここで、
\(\Theta=\frac{\displaystyle\partial u}{\displaystyle\partial x}+\frac{\displaystyle\partial v}{\displaystyle\partial y}+\frac{\displaystyle\partial w}{\displaystyle\partial z}=div \bf{v}\):体積膨張
\(-\frac{\displaystyle2}{\displaystyle3}\mu\Theta\):圧縮性によるひずみ応力
\(2\mu\frac{\displaystyle\partial u}{\displaystyle\partial x}\):垂直応力
3. ナビエ・ストークスの方程式

粘性により生じる応力と流体の運動(変形速度)を関連付けることができました。それではこれを運動方程式に組み入れてみます。
式(12)、式(13)からx方向に働く力は、
\[ \begin{cases}
yz面:-\sigma_{xx}dydz+\left[ \sigma_{xx}+\left( \partial \sigma_{xx}/\partial x \right) dx \right] dydz = \left( \partial \sigma_{xx}/\partial x \right)dxdydz
\\
zx面:-\tau_{yx}dzdx+\left[ \tau_{yx}+\left( \partial \tau_{yx}/\partial y \right) dy \right] dzdx = \left( \partial \tau_{yx}/\partial y \right)dxdydz
\\
xy面:-\tau_{zx}dxdy+\left[ \tau_{zx}+\left( \partial \tau_{zx}/\partial z \right) dz \right] dydx = \left( \partial \tau_{yx}/\partial z \right)dxdydz
\end{cases} ・・・(14)\]
単位体積あたりでは\(dxdydz=1\)となるので、式(14)の総和は、
\[
\begin{eqnarray}
&&\frac{\displaystyle \partial \sigma_{xx}}{\displaystyle \partial x}+\frac{\displaystyle \partial \tau_{yx}}{\displaystyle \partial y}+\frac{\displaystyle \partial \tau_{zx}}{\displaystyle \partial z}
\\
&=&\frac{\displaystyle \partial }{\displaystyle \partial x}\left( -p-\frac{\displaystyle 2}{\displaystyle 3}\mu\Theta+2\mu\frac{\displaystyle \partial u}{\displaystyle \partial x} \right)
+\frac{\displaystyle \partial }{\displaystyle \partial y}\mu\left( \frac{\displaystyle \partial v}{\displaystyle \partial x}+\frac{\displaystyle \partial u}{\displaystyle \partial y} \right)
+\frac{\displaystyle \partial }{\displaystyle \partial z}\mu\left( \frac{\displaystyle \partial u}{\displaystyle \partial z}+\frac{\displaystyle \partial w}{\displaystyle \partial x}\right) \\
&=&-\frac{\displaystyle \partial p}{\displaystyle \partial x}-\frac{\displaystyle 2}{\displaystyle 3}\mu\frac{\displaystyle \partial \Theta}{\displaystyle \partial x}+2\mu\frac{\displaystyle \partial^2 u}{\displaystyle \partial x^2}+\mu\left( \frac{\displaystyle \partial^2 v}{\displaystyle \partial x \partial y}+\frac{\displaystyle \partial^2 u}{\displaystyle \partial y^2} \right)+\mu\left( \frac{\displaystyle \partial^2 u}{\displaystyle \partial z^2}+\frac{\displaystyle \partial^2 w}{\displaystyle \partial x\partial z} \right) \\
&=&-\frac{\displaystyle \partial p}{\displaystyle \partial x}-\frac{\displaystyle 2}{\displaystyle 3}\mu\frac{\displaystyle \partial \Theta}{\displaystyle \partial x}+\mu\left( \frac{\displaystyle \partial^2 u }{\displaystyle \partial x^2}+\frac{\displaystyle \partial^2 v }{\displaystyle \partial x\partial y}+\frac{\displaystyle \partial^2 w}{\displaystyle \partial x\partial z} \right)+\mu\left( \frac{\displaystyle \partial^2 u}{\displaystyle \partial x^2}+\frac{\displaystyle \partial^2u }{\displaystyle \partial y^2 }+\frac{\displaystyle \partial^2 u}{\displaystyle \partial z^2} \right) \\
&=&-\frac{\displaystyle \partial p}{\displaystyle \partial x}-\frac{\displaystyle 2}{\displaystyle 3}\mu\frac{\displaystyle \partial \Theta}{\displaystyle \partial x}+\mu\frac{\displaystyle \partial \Theta}{\displaystyle \partial x}+\mu\left( \frac{\displaystyle \partial ^2 u}{\displaystyle \partial x^2}+\frac{\displaystyle \partial^2u }{\displaystyle \partial y^2}+\frac{\displaystyle \partial ^2 u}{\displaystyle \partial z^2} \right)\\
&=&-\frac{\displaystyle \partial p}{\displaystyle \partial x}+\frac{\displaystyle 1}{\displaystyle 3}\mu\frac{\displaystyle \partial \Theta}{\displaystyle \partial x}+\mu\left( \frac{\displaystyle \partial ^2 u}{\displaystyle \partial x^2}+\frac{\displaystyle \partial^2u }{\displaystyle \partial y^2}+\frac{\displaystyle \partial ^2 u}{\displaystyle \partial z^2} \right)
\end{eqnarray} ・・・(15)
\]
式(14)を式(9)の圧力項の代わりに代入するとx方向の運動方程式は、
\[
\frac{\displaystyle Du}{\displaystyle Dt}=F_x-\frac{\displaystyle 1}{\displaystyle \rho }\frac{\displaystyle \partial p}{\displaystyle \partial x}+\frac{\displaystyle 1}{\displaystyle 3}\frac{\displaystyle \mu}{\displaystyle \rho}\frac{\displaystyle \partial \Theta}{\displaystyle \partial x}+\frac{\displaystyle \mu }{\displaystyle \rho}\left( \frac{\displaystyle \partial^2 u }{\displaystyle \partial x^2}+\frac{\displaystyle \partial^2 u}{\displaystyle \partial y^2}+\frac{\displaystyle \partial^2 u}{\displaystyle \partial z^2} \right) ・・・(16)
\]
同様に、y,z方向に対して
\[
\frac{\displaystyle Dv}{\displaystyle Dt}=F_y-\frac{\displaystyle 1}{\displaystyle \rho }\frac{\displaystyle \partial p}{\displaystyle \partial y}+\frac{\displaystyle 1}{\displaystyle 3}\frac{\displaystyle \mu}{\displaystyle \rho}\frac{\displaystyle \partial \Theta}{\displaystyle \partial y}+\frac{\displaystyle \mu }{\displaystyle \rho}\left( \frac{\displaystyle \partial^2 v }{\displaystyle \partial x^2}+\frac{\displaystyle \partial^2 v}{\displaystyle \partial y^2}+\frac{\displaystyle \partial^2 v}{\displaystyle \partial z^2} \right) ・・・(16)
\]
\[
\frac{\displaystyle Dw}{\displaystyle Dt}=F_z-\frac{\displaystyle 1}{\displaystyle \rho }\frac{\displaystyle \partial p}{\displaystyle \partial z}+\frac{\displaystyle 1}{\displaystyle 3}\frac{\displaystyle \mu}{\displaystyle \rho}\frac{\displaystyle \partial \Theta}{\displaystyle \partial z}+\frac{\displaystyle \mu }{\displaystyle \rho}\left( \frac{\displaystyle \partial^2 w }{\displaystyle \partial x^2}+\frac{\displaystyle \partial^2 w}{\displaystyle \partial y^2}+\frac{\displaystyle \partial^2 w}{\displaystyle \partial z^2} \right) ・・・(16)
\]
または、ベクトル表示で、
\[
\frac{\displaystyle D\bf{v}\rm}{\displaystyle \partial }=\bf{F}\rm-\frac{\displaystyle 1}{\displaystyle \rho}{\rm grad} \it{}p+\frac{\displaystyle 1}{\displaystyle 3}\frac{\displaystyle \mu}{\displaystyle \rho}{\rm grad} \it{}\Theta+\frac{\displaystyle \mu}{\displaystyle \rho}\nabla^2 \bf{v}\rm ・・・(16)’
\]
ここで、
\[
\begin{eqnarray}
&&ラプラシアン:\nabla^2=\frac{\displaystyle \partial ^2}{\displaystyle \partial x^2}+\frac{\displaystyle \partial^2 }{\displaystyle \partial y^2}+\frac{\displaystyle \partial^2 }{\displaystyle \partial z^2}
&&勾配{\rm grad}=\left( \frac{\displaystyle \partial }{\displaystyle \partial x},\frac{\displaystyle \partial }{\displaystyle \partial y},\frac{\displaystyle \partial }{\displaystyle \partial z} \right)
\end{eqnarray}
\]
式(16)および式(16)’をナビエ・ストークスの方程式といいます。
このうち、粘性による項は\( (\mu/\rho)\cdot\nabla^2 \bf{v}\rm\)で表わされます。
動粘性係数:\(\mu/\rho=\nu\) \(1[m^2/sec]=10St(ストークス)\)
流体が非圧縮の時、体積変化がないから、\(div \bf{v}=0 \)となり、
\[
\frac{\displaystyle D\bf{v}\rm}{\displaystyle \partial }=\bf{F}\rm-\frac{\displaystyle 1}{\displaystyle \rho}{\rm grad} \it{}p+\frac{\displaystyle \mu}{\displaystyle \rho}\nabla^2 \bf{v}\rm ・・・(16)”
\]

希薄流体や音速を超える高速流体以外では、この非圧縮性流体におけるナビエ・ストークス方程式が適用できます。

