渦度と循環の解説は式のみが多く、いまいちピンとこない方もいると思います。今回、図を交えて解説します。
1. 渦度
渦度とは、一言で言うと「流体の局所的な回転の強さ」です。
上記の記事内の式(8)の式
\[
\omega = \begin{pmatrix} \xi \\ \eta \\ \zeta \end{pmatrix}=
\begin{pmatrix} \frac{\displaystyle \partial w}{\displaystyle \partial y} -\frac{\displaystyle \partial v}{\displaystyle \partial z}
\\
\frac{\displaystyle \partial u}{\displaystyle \partial z}-\frac{\displaystyle \partial w}{\displaystyle \partial x}
\\
\frac{\displaystyle \partial v}{\displaystyle \partial x}-\frac{\displaystyle \partial u}{\displaystyle \partial y}
\end{pmatrix}
\]
について、
\(\omega=0\)の流れを渦なし流れ(irrotational flow)
\(\omega\neq0\)の流れを渦あり流れ(rotational flow)
と言います。
これをイメージでお伝えすると次の図の様になります。
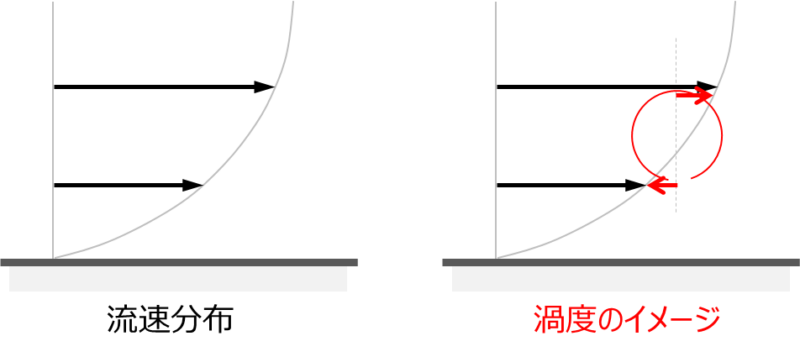
イメージを数式で表現していきたいと思います。
\(\omega=0\)の時
\[
\frac{\displaystyle \partial w}{\displaystyle \partial y}=\frac{\displaystyle \partial v}{\displaystyle \partial z}, \frac{\displaystyle \partial u}{\displaystyle \partial z}=\frac{\displaystyle \partial w}{\displaystyle \partial x}, \frac{\displaystyle \partial v}{\displaystyle \partial x}=\frac{\displaystyle \partial u}{\displaystyle \partial y}
\]
これは、次式が全微分をとるための必要十分条件(以下補足)なので、次のようなスカラー関数\(\phi\)の全微分が得られます。
\[d\phi = udx+vdy+wdz ・・・(1)\]
微分方程式\(M(x,y)dx+N(x,y)dy=0\)が
\(\frac{\displaystyle \partial M}{\displaystyle \partial y}=\frac{\displaystyle \partial N}{\displaystyle \partial x}\)
という性質を持っているならば
\(df = \frac{\displaystyle \partial f}{\displaystyle \partial x}dx+\frac{\displaystyle \partial f}{\displaystyle \partial y}dy\)
\(f(x,y)\)は\(xとy\)で微分可能である。
式(1)を\(x\)で偏微分(\(x\)方向の変化分以外は定数)すると
\[\frac{\displaystyle \partial \phi}{\displaystyle \partial x}
=u\frac{\displaystyle \partial x}{\displaystyle \partial x}+v\frac{\displaystyle \partial y}{\displaystyle \partial x}+w\frac{\displaystyle \partial z}{\displaystyle \partial x}\\
=u ・・・(2)
\]
したがって、
\[u=\frac{\displaystyle \phi}{\displaystyle x}, v=\frac{\displaystyle \phi}{\displaystyle y}, w=\frac{\displaystyle \phi}{\displaystyle z} ・・・(2)\]
となるので、速度ベクトルは
\[{\bf v}=(u,v,w)=\left( \frac{\displaystyle \partial \phi}{\displaystyle \partial x},\frac{\displaystyle \partial \phi}{\displaystyle \partial y},\frac{\displaystyle \partial \phi}{\displaystyle \partial z} \right)=\nabla\phi={\rm grad}\phi\]
この時、関数\(\phi\)を速度ポテンシャル(velocity potential)と言います。

すなわち、渦なし流れ(\(\omega=0\))では、流れ場をスカラー関数で表現できる(流れを解析的に解ける)ことを表しています。
2. 循環
次の記事内でも少し触れましたが、改めてイメージから数式に落としていきたいと思います。

翼に揚力が働くのは「翼周りに循環があるから」と表現されます。上図の様に無限遠の流速\(V\)の環境において、翼の上下には\(v\)分だけ速度に違いがあるとします。相対的に見た場合、\(v\)の分だけ回転するようにベクトルが発生している状態です。(揚力発生原理は上記の記事で解説していますので割愛します)上記のイメージを持ちつつ、次の一般論の解説をご覧ください。
次の図の様に、曲線\(C\)について、\(C\)の線素\(ds\)に沿う流れの成分\(v_s\)(接線方向の成分)の積分を考えます。
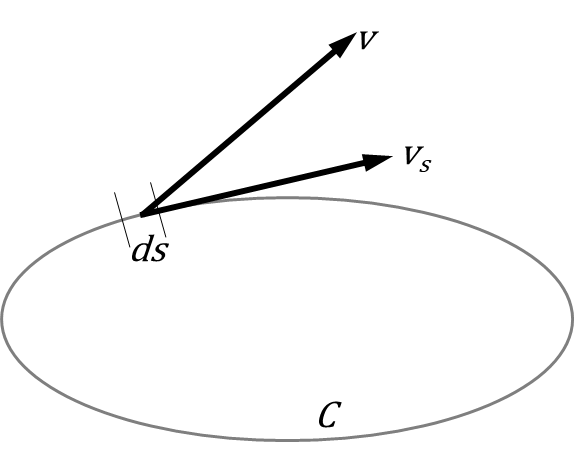
線分ベクトル\(d{\bf s}\)と流れのベクトル\({bf v}\)の\(ds\)に平行な成分\(v_s\)の積は、二つのベクトルの内積\({\bf v}\cdot d{\bf s}=v_s ds\)であるので(内積:同一方向成分をかける)
\[\begin{eqnarray}
I&=&\int_C v_s ds \\
&=&\int_C {\bf v}\cdot d{\bf s} \\
&=&\int_C({\bf i}u+{\bf j}v+{\bf k}w)\cdot({\bf i}dx+{\bf j}dy+{\bf k}dz) \\
&=&\int_C(udx+vdy+wdz)
\end{eqnarray}\]
これは\(C\)に沿う流れを表します。
曲線\(C\)が閉曲線のとき、この積分を\(\Gamma(C)\)と書き、\(C\)についての循環(circulation)と言います。
\[\begin{eqnarray}
\Gamma(C)&=&\oint v_s ds \\
&=&\oint {\bf v}d{\bf s} \\
&=&\oint (udx+vdy+wdz)
\end{eqnarray} ・・・(3)\]

この「循環」こそが翼周りで揚力が発生する際に生じている現象であり、クッタ・ジューコフスキーの定理で使われている循環\(\Gamma\)となります。


