振動の中で最も基本的な単振動について解説します。
1.復元力
つり合い状態にある物体をずらすと、そのずれに比例して元に戻ろうとする力が働きます。これを復元力とよび、復元力による運動を単振動といいます。ここで次の図のようなモデルを考えます。
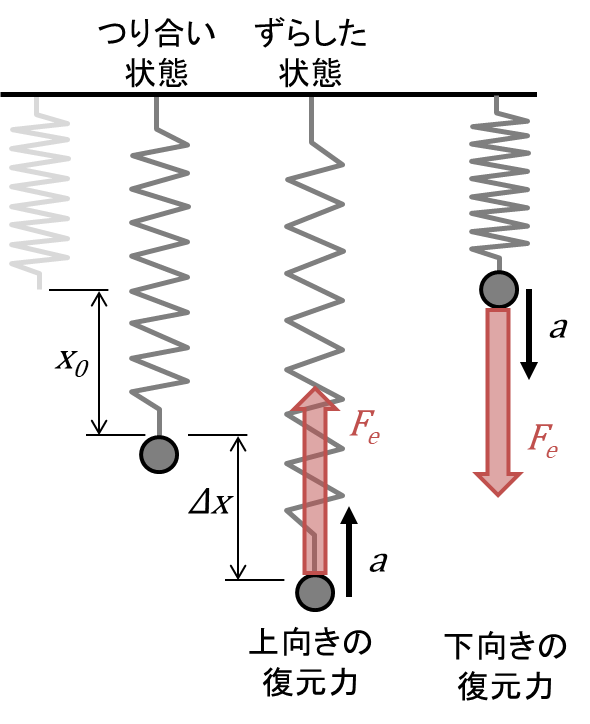
ばねに 錘(質量\(m\))をつけて重力\(mg\)とばね力\(kx_0\)が釣り合った状態があります。\(\Delta x\)だけ下に引っ張って「ずらした状態」を作ります。すると、 錘には上向きの復元力\(F\)が働き、 錘が上に上がりきると下向きの復元力\(F\)が働きます。復元力\(F\)は、重力\(mg\)とばね力\(-k(x_0+\Delta x)\)の合計なので次の様に表されます。
\[
F=mg-k(x_0+\Delta x)
\]
ここで\(mg=k x_0\)なので、
\[
F=-k\Delta x
\]
となり、復元力はつり合い状態からずらした量に比例することがわかります。
2. 単振動の式
先ほどのずらした状態から錘は上下に振動します。すると次の図の様に\(\Delta x\)の幅の分だけ上下に運動を繰り返します。この時の\(\Delta x\)を振幅とよび、この運動を振動とよびます。
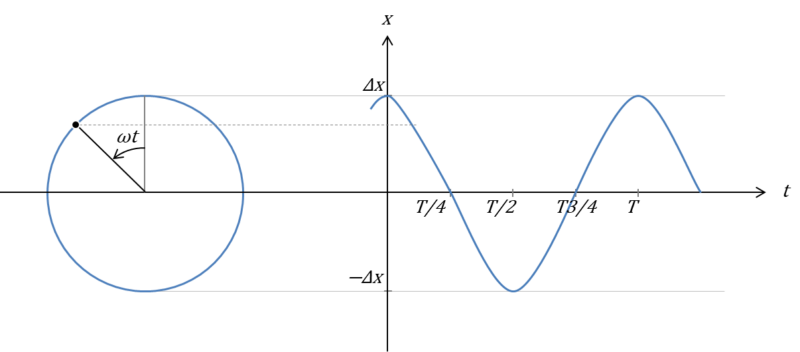
半径\(\Delta x\)、角速度\(\omega\)の等速円運動で模擬できることがわかります。ここで、等速円運動の向心加速度\(a=-\omega^2r\)であり、半径\(r=x\)と置くと
\[
a=-\omega^2x
\]
したがって向心力\(F_c\)は
\[
F_c=ma=-m\omega^2x
\]
向心力とばね力を同様にとらえると
\[
kx=\omega^2x
\]
となり
\[
\omega=\sqrt{k/m}
\]
と表すことができます。ここで、\(\omega\)を角振動数とよびます。ここで1回の周期の時間Tにおける角度は\(\omega T=2\pi\)であることから
\[
T=2\pi\sqrt{\frac{\displaystyle m}{\displaystyle k}}
\]
また、振動数(周波数)\(f=1/T\)であることから
\[
f=\frac{\displaystyle 1}{\displaystyle 2\pi}\sqrt{k/m}
\]
と表すことができます。


