減衰振動｜実在世界の振動のモデル化と式の導出

　単振動のモデルは一定の状態で続く振動のため、実在世界には存在しません。ここでは、より実態に即した減衰していく振動について解説します。

1. 減衰振動のモデル
2. 減衰振動の運動方程式

1. 減衰振動のモデル

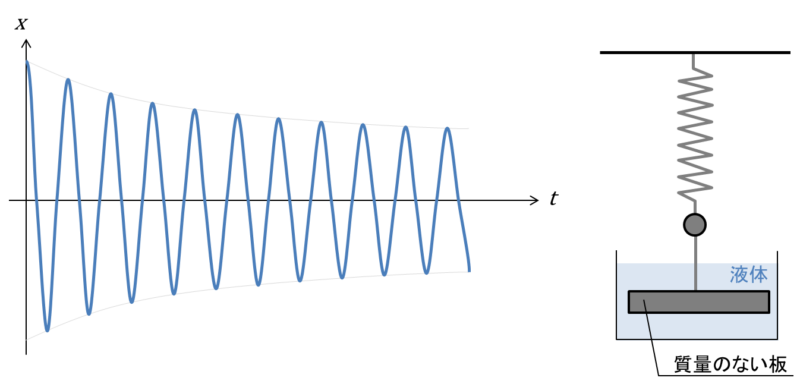
　グラフに示すように、現実世界の振動では流体（空気や液体など）や固体の抵抗を受けて振動のエネルギーが失われ（厳密には熱エネルギーに変換されて散逸します）、減衰していきます。これを簡単なモデルで表わしたものを上の図に示しました。単振動で解説したバネと錘に”液体”と”質量のある板”を加えました。

　減衰を大きくするには、液体の抵抗を大きくすればよく、そのためには質量のある板を大きくします。あるいは、液体を粘度の高いものに交換してもよいです（例えば、水から油に交換する）。

この流体を使って抵抗を生じさせて振動を減衰させる装置を「ダッシュポット」や「ダンパー」と呼びます。

2. 減衰振動の運動方程式

　１．で解説した抵抗は速度\(v\)に比例します。この抵抗力を\(-mcv\)（\(c\)：定数、\(v\)：速度）とし、復元力を\(-kx=-m\omega^2x\)とするとニュートンの運動方程式は次のように表せます。
\[
m\frac{\displaystyle d^2x}{\displaystyle dt^2}=-kx-2mc\frac{\displaystyle x}{\displaystyle dt}=-m\omega^2 x-2mc\frac{\displaystyle dx}{\displaystyle dt}
\]

上式を整理すると次のようになります。
\[
\frac{\displaystyle d^2x}{\displaystyle d^2 t}+2c\frac{\displaystyle dx}{\displaystyle dt}+\omega^2 x=0
\]

　減衰の大小で次の３つの定義がされており、一般解が導かれています。

減衰振動：抵抗が小さい場合（\(\omega>c\)）
\[x=Ae^{-ct}cos[\sqrt{\omega^2-c^2}t+\alpha]\]
過減衰　：抵抗が大きく振動しない場合（\(\omega<c\)）
\[x=Ae^{-(c-\beta)t}+Be^{-(c+\beta)t},\,\,\beta=\sqrt{c^2-\omega^2}\]
臨界減衰：減衰振動と過減衰の間（\(\omega=c\)）
\[x=(A+Bt)e^{-ct}\]

ここで、\(A,B,\alpha\)は任意の定数です。