錘を糸でつるしたような振り子の事例を単振動の考え方を基に解説します。
モデルと基礎式
(1)単振り子のモデル
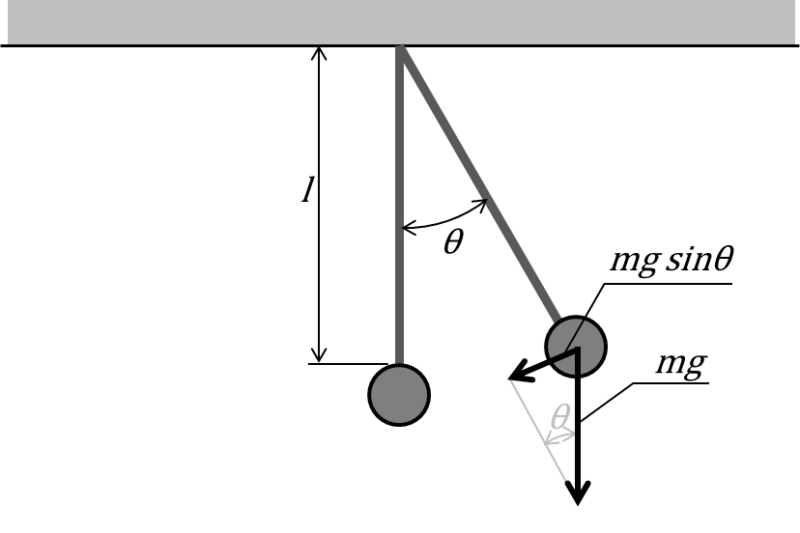
図の様に長さ\(l\)の糸に重さ\(m\)の錘をつけて振動させるモデルを単振り子とよびます。錘を運動させる力は糸と直行する方向に働くため、糸が\(\theta\)だけずれた状態だと
\[
F=-mg sin\theta
\]
となります。
(2) 単振り子の運動方程式
最下点から錘の移動距離は円弧の長さのため\(l\theta\)と表せます。したがって、糸に直行する方向の錘の加速度のは\(d^2(l\theta)/dt^2\)、\(l\)は定数のため微分の外に出すと\(ld^2\theta /dt^2\)となります。この考え方を基に運動方程式をたてると
\[
ml\frac{\displaystyle d^2 \theta}{\displaystyle dt^2}=-mg sin \theta
\]
したがって
\[
\frac{\displaystyle d^2 \theta}{\displaystyle dt^2}= -\frac{\displaystyle g}{\displaystyle l}sin \theta
\]
となります。
ここで、仮に\(\theta\)が1に対して極小さい場合、\(sin\theta ≒ \theta\)と置くことができるため、上式は次のようになります。
\[
\frac{\displaystyle d\theta^2}{\displaystyle d^2 t}=-\frac{\displaystyle g}{\displaystyle l}\theta
\]
ここで、上式は次の記事で導出したものと同じ形になります。
すなわち、上の記事内のばね定数\(k\)を\(mg/l\)で置き換えると周波数\(f\)は
\[
f=\frac{\displaystyle 1}{\displaystyle 2\pi}\sqrt{\frac{\displaystyle g}{\displaystyle l}}
\]
と表すことができます。


