
沸騰のメカニズムから伝熱の特性式を解説します。
1. 核沸騰のメカニズム
伝熱面上に存在する微小な傷や穴(キャビティ)を介して沸騰が生じます。
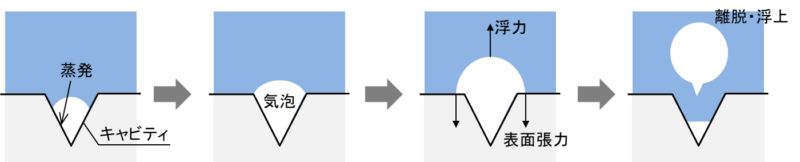
最初に活性化する(気泡を生じる)キャビティの大きさは30~40μm程度です。伝熱面熱流束が増えるにつれて、活性化するキャビティの大きさが広がっていきます。
核沸騰により、次のように熱移動が生じます。
① 過熱液の蒸発による潜熱移動
② 気泡に付着した過熱液の持ち去り
③ 気泡離脱に伴う境界層の攪拌効果
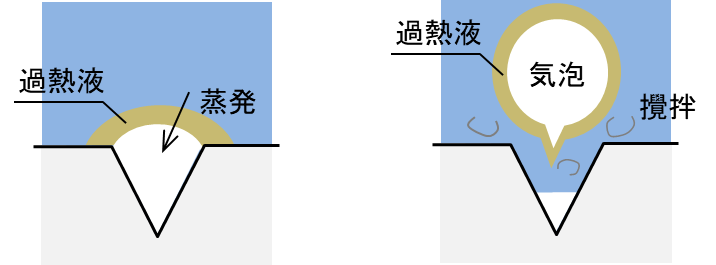

これら3つが重畳して、核沸騰時には非常に高い熱伝達率が実現されます。
2. 核沸騰伝熱の整理式
核沸騰による熱移動は、一般には伝熱面の過熱度\(\Delta T_{sat}\)と発泡点(活性化されたキャビティ)の密度\(n [1/m^2]\)に依存し、次の関係式が成立します。
\(
q_w = C_n \Delta T_{sat}^a \cdot n^b
\)
ここで、\(a=1~2、b=0.25~0.42、C_n:比例定数\)です。
主な飽和プール核沸騰の熱伝達整理式
・Kutateladze(クタテラッゼ)の式
\(
\frac{\displaystyle h l_a}{\displaystyle \lambda_l}=7.0\times 10^{-4}\cdot Pr_l^{0.35}\left[ \frac{\displaystyle q_w}{\displaystyle L\rho_v}\frac{\displaystyle l_a}{\displaystyle v_l} \right]^{0.7}\cdot \left[\frac{\displaystyle p l_a}{\displaystyle \sigma}\right]^{0.7} ・・・(1)
\)
・Rohsenow(ローゼナウ)の式
\(
\frac{\displaystyle C_{pl}\Delta T_{sat}}{\displaystyle L}=C_{fs}\cdot \left[ \frac{\displaystyle q_w l_a}{\displaystyle L \mu _l} \right]^{0.33}\cdot Pr_l^s ・・・(2)
\)
ここで、上式(1),(2)中の諸量は、次の通りです。
\(l_a = \sqrt{\frac{\displaystyle \sigma}{\displaystyle g(\rho_l-\rho_v)}}\):これをラプラス長さと言います
\(L:蒸発潜熱[J/kg]、\sigma:表面張力[N/m]、P:系圧力[Pa]\)
添字 \(v:蒸気、l:液\)
また、式(2)のプラントル数\(Pr_l\)の指数\(s\)は、\(1\)(水)\(1.7\)(その他の液体)
\(C_{fs}=0.00225~0.027\)(特に、水-銅、水-ステンレス鋼では0.013)

上の他にも数多くの整理式が提案されています。それらの式を用いて\(q\)を計算すると、各式によって一桁程度値が異なることに注意してください。核沸騰伝熱は、伝熱表面の性状(粗さ、表面仕上げ)によって大きく変化(キャビティの数が異なる)、加えて液体どの濡れ、表面の経変変化などを考慮すると、これらを全て取り込んだ整理式を提案することは不可能に近いです。
要するにあてにならないので実際に実験をやってみるしかないのです。
3. 核沸騰の限界熱流束(バーンアウト熱流束)
ボイラや原子炉燃料棒では、この限界熱流束を越えると機器の焼損が生じるため非常に危険です。したがって、限界熱流束がどの程度の値になるのかを見積もることは工業的に重要となります。
伝熱面付近に多数の蒸気泡が形成され、この蒸気泡の離脱・上昇に抗して、液体が伝熱面に到達できなくなり、伝熱面が乾いた状態(ドライアウト)になります。

限界熱流束の予測式(水平上向き面上のプール沸騰)
・Zuber(ズーバー)の式(飽和沸騰に適用)
\(
q_{c0}=0.138(\rho_v L)\left[ \frac{\displaystyle g\sigma(\rho_l-\rho_v)}{\displaystyle \rho_v^{0.2}} \right]^{1/4}\left[ \frac{\displaystyle \rho_l+\rho_v}{\displaystyle \rho_l} \right]^{1/2} ・・・(3)
\)
・Kutateladzeの式(サブクール沸騰に適用)
\(
\frac{\displaystyle q_c}{\displaystyle q_{c0}}=1+0.065\left( \frac{\displaystyle \rho_l}{\displaystyle \rho_v} \right)^{0.8}\cdot \left( \frac{\displaystyle C_{pl}\Delta T_{sub}}{\displaystyle L} \right) ・・・(4)
\)
ここで、\(\Delta T_{sub}=(T_{sat}-T_l)、q_{c0}:式(3)より算出した飽和沸騰の限界熱流束\)です。なお、これらの式は実験値と比較的良い一致を示すといわれています。
4. 膜沸騰
膜沸騰とは、伝熱面の温度が高くなると(数百℃)、伝熱面全体が蒸気膜によって覆われるようになります。熱はこの蒸気膜内を、伝導・対流・放射によって移動します。
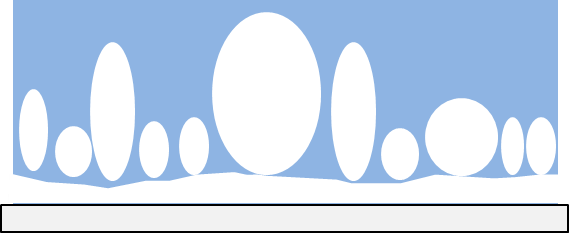

膜沸騰は、鋼の熱間圧延や焼入れなどで見られます。
膜沸騰では、伝熱面の粗さや濡れなどの影響が無視できることから、メカニズム的には核沸騰よりも単純です。したがって、解析的な取り扱いは比較的容易となり、得られた解も比較的実験値に合います。


