並列な熱流れに対する熱通過率についてはどの教科書でも触れられていないため、熱通過率の式の導出を解説したいと思います。
1. 並列な熱流れのモデル
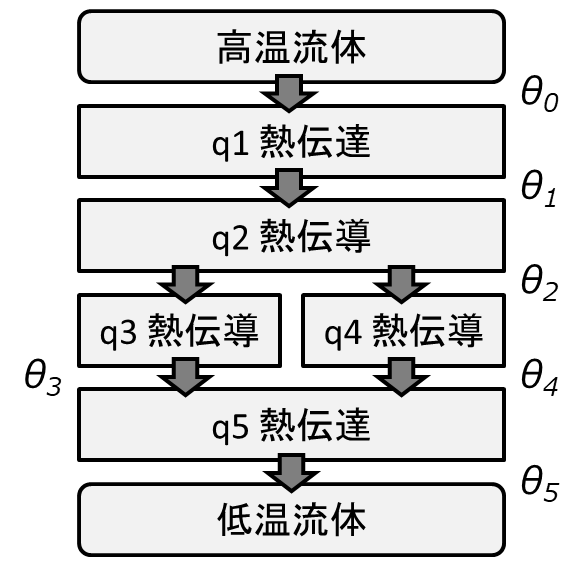
次のように熱伝達と熱伝導からなる並列な熱流れをモデルにします。
ここで、\(q\):熱流束[W/m2]、\(\theta\):温度[K]。
2. 各熱流束の定義式
\(\alpha\):熱伝達率[W/mK]、\(\lambda\):熱伝導率[W/mK]、\(L\):距離[m]とすると、各熱流束は次のように定義できます。
\[q1=\alpha_1(\theta_0-\theta_1)\]
\[q2=\frac{1}{L_2}\lambda_2(\theta_1-\theta_2)\]
\[q3=\frac{1}{L_2}\lambda_3(\theta_2-\theta_3)\]
\[q4=\frac{1}{L_4}\lambda_4(\theta_2-\theta_4)\]
ここで、並列に流れた熱が合流することから便宜上\(\theta_3=\theta_4\)と置くと
\[q5=\alpha_5\lambda(\theta_4-\theta_5)\]
3. 熱伝達率の導出
定常状態であれば\(q_1=q_2=(q_3+q_4)=q5となり、熱流束は直列に流れる箇所であればどの断面でも同じ値をとります。並列に流れる箇所の総和が、直列に流れる箇所と同じ値をとります。これは電気と同じですね。
並列に流れる箇所の式を\(\theta_3=\theta_4\)とおいて表現すると
\[q_3+q_4=(\frac{\lambda_3}{L_3}+\frac{\lambda_4}{L_4})(\theta_2-\theta_3)\]
となり並列に流れる熱を和で表現します。
次に、一般的な熱伝達率を求めるのと同様に次のように式変形していきます。
\[\begin{eqnarray}
\theta_0-\theta_5
&=&(\theta_0-\theta_1)+(\theta_1-\theta_2)+(\theta_2-\theta_3)+(\theta_3-\theta_5)
\\
&=&\frac{q}{\alpha_1}+q\frac{L_2}{\lambda_2}+\frac{q}{\frac{\lambda_3}{L_3}+\frac{\lambda_4}{L_4}}+\frac{q}{\alpha_5}
\end{eqnarray}\]
上式を\(q=\)の形となるように変形すると
\[q=(\theta_0-\theta_5)\frac{1}{\frac{1}{\alpha_1}+\frac{L_2}{\lambda_2}+\frac{1}{\frac{\lambda_3}{L_3}+\frac{\lambda_4}{L_4}}+\frac{1}{\alpha_5}}\]
したがって、熱通過率\(k\)は
\[k=\frac{1}{\frac{1}{\alpha_1}+\frac{L_2}{\lambda_2}+\frac{1}{\frac{\lambda_3}{L_3}+\frac{\lambda_4}{L_4}}+\frac{1}{\alpha_5}}\]
となります。
4. まとめ
熱通過率は電気の流れと同様に熱の流れをイメージすれば、簡単なモデルを組み立てることができます。いきなり高度なシミュレーション解析をするのではなく、まずは、こういったモデルを作って当たりをつけてから詳細な検討に移ることで、実際の熱の流れを自在に制御できるようになるでしょう。
