
垂直な加熱平板に沿う自然対流の基礎方程式である運動量式とエネルギー式を導出します。
1. 運動量式
図の様に垂直な加熱平板に沿う自然対流を考えます。2次元定常層流、密度\(\rho\)以外の流体の物性値は一定、境界層近似が成立する、という条件のもとで、運動量の式は次のように表せます。
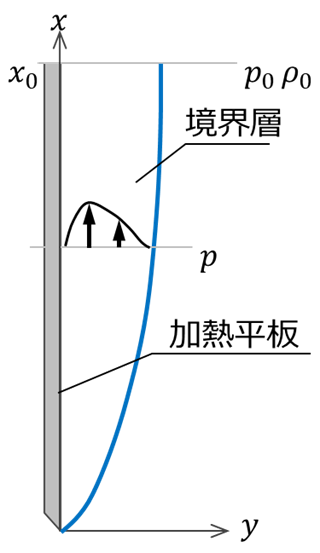
<x方向の運動量式>
\[
\rho\left( u \frac{\displaystyle \partial u}{\displaystyle \partial x}+v \frac{\displaystyle \partial u}{\displaystyle \partial y} \right)=-\frac{\displaystyle \partial p}{\displaystyle \partial x}-\rho g + \mu\frac{\displaystyle \partial^2 u}{\displaystyle \partial y^2}
・・・(1)\]
<y方向の運動量式>
\[
-\frac{\displaystyle \partial p}{\displaystyle \partial y}=0 ・・・(2)
\]
式(2)は境界層内の圧力が、任意の断面\(x\)において一定であることを示しています。この性質を利用すると、式(1)右辺の圧力pは、基準となる位置\(x=x_0\)における圧力を\(p_0\)とすると、
\[p=p_0+\rho_0 g(x-x_0)\]
で表わされます。これより圧力勾配\(-\partial p/\partial x\)を求めると、
\[-\frac{\displaystyle \partial p}{\displaystyle \partial x}=\rho_0 g ・・・(3)\]
この式(3)を式(1)に代入すると、最終的に式(1)は次のようになります。
\[
\rho\left(u\frac{\displaystyle \partial u}{\displaystyle \partial x}+v\frac{\displaystyle \partial u}{\displaystyle \partial y}\right)=g(\rho_0-\rho)+\mu\frac{\displaystyle \partial^2 u}{\displaystyle \partial y^2} ・・・(4)
\]
式(4)を直接解くには、流体の密度\(\rho\)および\(\rho_0\)の値を温度の関数として予め与える必要があります。これは実際に計算を行う際には、かなり不便であるので、つぎのように体積膨張係数\(\beta\)を使って、密度を温度の関数として陽的に表す方法が一般に採用されます。
\[
\beta = \frac{\displaystyle 1}{\displaystyle V} \left( \frac{\displaystyle \partial V}{\displaystyle \partial T} \right) _p \simeq \frac{\displaystyle 1}{\displaystyle V_0}\frac{\displaystyle V-V_0}{\displaystyle T-T_0} =\rho _{\infty}\frac{\displaystyle 1/\rho – 1/\rho _0}{\displaystyle T-T_0}= \frac{\displaystyle \rho_0-\rho}{\displaystyle \rho (T-T_0) }
・・・(5)
\]
この関係より、\(\rho(\rho_0-\rho)=\rho g \beta (T-T_0)\)、これを式(4)に代入すると、式(4)は
\[
\rho\left( u\frac{\displaystyle \partial u}{\displaystyle \partial x}+v\frac{\displaystyle \partial u}{\displaystyle \partial y} \right) = \rho g \beta (T-T_0)+\mu \frac{\displaystyle \partial^2 u}{\displaystyle \partial y^2} ・・・(6)
\]

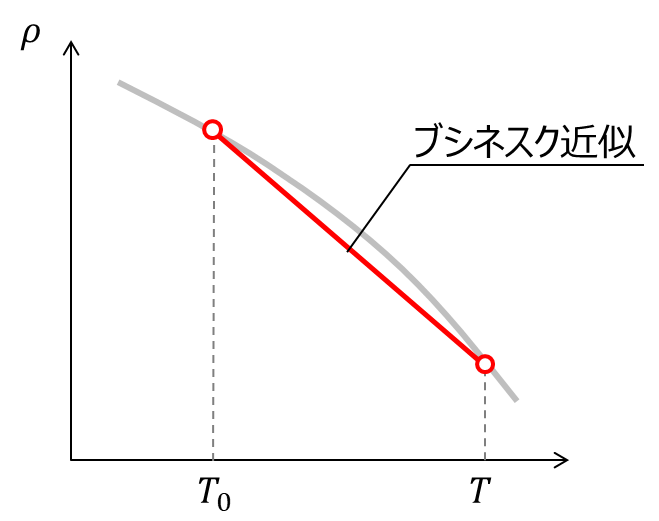
式(5)の近似をブシネスク近似といいます。この近似が成立するのは、あくまでも密度\(\rho\)が温度\(T\)に比例して直線的に変化する場合です。
2. 熱エネルギー式
自然対流に対する熱エネルギー式は、強制対流に対するそれと全く同一で、上の体系についていは次式が成立します。
\[
\rho C_p \left( u\frac{\displaystyle \partial T}{\displaystyle \partial x}+v\frac{\displaystyle \partial T}{\displaystyle \partial y} \right)=\lambda \frac{\displaystyle \partial^2 T}{\displaystyle \partial y^2} ・・・(7)
\]
3. 基礎方程式の解法
式式(6)、式(7)を解くには次の3つの方法があります。
- プロフィル法
- 相似解法
- 数値解法

いずれにしても式(6)、式(7)を解くにはこれらを連立する必要があります。したがって、自然対流を解くことは、方程式が互いに独立して解ける強制対流よりも難しくなります。



