
乱流の定義と物理的な意味をレイノルズの実験による成り立ちから解説します。
1. 乱流の発生とレイノルズ応力
(1)レイノルズの実験
円管内の流れは、「圧力勾配 小、流量 少」の時、ハーゲン・ポアゾイユの公式に従います。「圧力勾配 大、流量 多」の時は、公式に従わず、下図の通り流体が流れにくくなります。
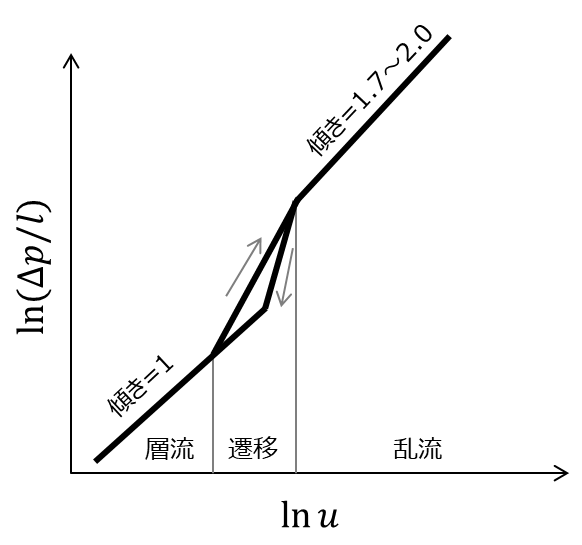
この現象をレイノルズは、流れの可視化によって次の図の様にとらえました。図中の(a)の様に流体粒子が層状に秩序正しく流れる状態を層流(ポアゾイユ流)、図中の(b)の様に不規則に混合しながら流れる状態を乱流といいます。
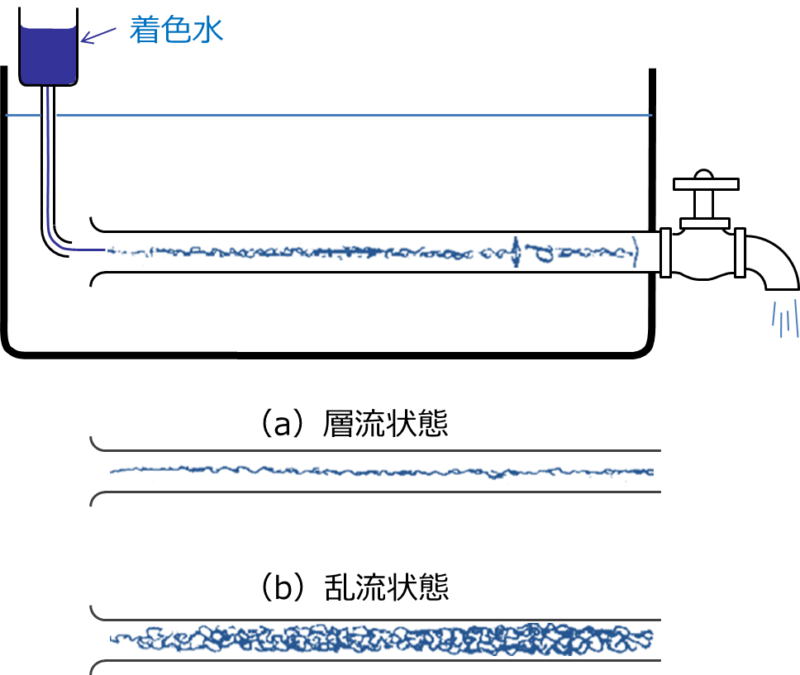
層流から乱流への遷移は、レイノルズ数が
\[Re=UD/\nu=2300\]
を超えると起こります。(\(U:平均流速、D:管内径、\nu:動粘性係数\))
これを臨界レイノルズ数\(Re_c\)と呼び、管の形状および水槽内の水の状態によって異なり、次に示すような範囲を持ちます。
\[1.6 \times 10^3 < Re_c < 2\times 10^5\]
(2)レイノルズ応力
乱流の速度成分を、平均速度(乱れの時間的スケールに比べて十分長い時間で平均)と、変動成分に分けて考えます。
\[\begin{cases}
u&=&\bar{u}+u’ \\
v&=&\bar{v}+v’ \\
w&=&\bar{w}+w’
\end{cases} ・・・」(1)\]
\(\bar{u},\bar{v},\bar{w}\):時間平均速度
\(u’,v’,w’\):変動速度
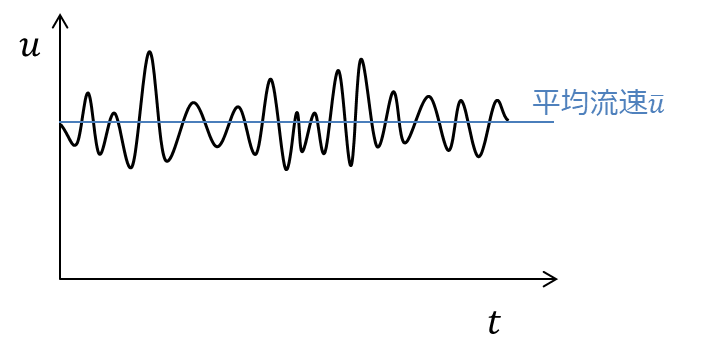
いま、平行平板間の流れについて考えると
\[\begin{cases}
u&=&\overline{u}+u’ \\
v&=&v’ \\
w=0
\end{cases} ・・・(2)\]
乱流中では、流れの混合作用による乱流せん断応力が働きます。次の図に示すように、\(y\)軸に垂直な単位面積、単位時間あたりの運動量\(\rho u’\)は\(y\)方向に\(v’\)で運ばれ、面\(dA\)の上側では\(\rho u’v’\)の運動量が増加します。このために、輸送された運動量に等しい応力が面\(dA\)に生じます。
\[\tau = -\rho \overline{u’v’} ・・・(3)\]
これをレイノルズ応力(Reynolds stress)とよびます。
粘性せん断応力と同様に、レイノルズ応力もテンソル量です。
\[
\begin{pmatrix}
\sigma_{xx} & \tau_{xy} & \tau{xx} \\
\tau_{yx} & \sigma{yy} & \tau_{yz} \\
\tau_{zx} & \tau_{zy} & \sigma_{zz}
\end{pmatrix}
=
\begin{pmatrix}
-\rho\overline{u’u’} & -\rho\overline{u’v’} &-\rho\overline{u’w’} \\
-\rho\overline{v’u’} & -\rho\overline{v’v’} &-\rho\overline{vw’} \\
-\rho\overline{w’u’} & -\rho\overline{w’v’} &-\rho\overline{w’w’}
\end{pmatrix}
・・・(4)\]
レイノルズはこの応力をナビエ・ストークス方程式から導きました。式(1)および\(p=\overline{p}+p’\)をナビ・エストークス方程式(次の関連記事の式(16)’)に代入して平均をとると、
\[\begin{cases}
\rho\left( \frac{\displaystyle \partial \bar{u}}{\displaystyle \partial t}+\bar{u}\frac{\displaystyle \partial \bar{u}}{\displaystyle \partial x}+\bar{v}\frac{\displaystyle \partial \bar{u}}{\displaystyle \partial y} +\bar{w}\frac{\displaystyle \partial \bar{u}}{\displaystyle \partial z}\right)
&=& \rho F_x – \frac{\displaystyle \partial \bar{p}}{\displaystyle \partial x}+\mu\nabla^2\bar{u}-p\left(\frac{\displaystyle \partial \overline{u’^2}}{\displaystyle \partial x}+\frac{\displaystyle \partial \overline{u’v’}}{\displaystyle \partial y} +\frac{\displaystyle \partial \overline{u’w’}}{\displaystyle \partial z} \right) \\
\rho\left( \frac{\displaystyle \partial \bar{v}}{\displaystyle \partial t}+\bar{u}\frac{\displaystyle \partial \bar{v}}{\displaystyle \partial x}+\bar{v}\frac{\displaystyle \partial \bar{v}}{\displaystyle \partial y} +\bar{w}\frac{\displaystyle \partial \bar{v}}{\displaystyle \partial z}\right)
&=& \rho F_y – \frac{\displaystyle \partial \bar{p}}{\displaystyle \partial y}+\mu\nabla^2\bar{v}-p\left(\frac{\displaystyle \partial \overline{u’v’}}{\displaystyle \partial x}+\frac{\displaystyle \partial \overline{v’^2}}{\displaystyle \partial y} +\frac{\displaystyle \partial \overline{v’w’}}{\displaystyle \partial z} \right) \\
\rho\left( \frac{\displaystyle \partial \bar{w}}{\displaystyle \partial t}+\bar{u}\frac{\displaystyle \partial \bar{w}}{\displaystyle \partial x}+\bar{v}\frac{\displaystyle \partial \bar{w}}{\displaystyle \partial y} +\bar{w}\frac{\displaystyle \partial \bar{w}}{\displaystyle \partial z}\right)
&=& \rho F_z – \frac{\displaystyle \partial \bar{p}}{\displaystyle \partial z}+\mu\nabla^2\bar{w}-p\left(\frac{\displaystyle \partial \overline{u’w’}}{\displaystyle \partial x}+\frac{\displaystyle \partial \overline{v’w’}}{\displaystyle \partial y} +\frac{\displaystyle \partial \overline{w’^2}}{\displaystyle \partial z} \right)
\end{cases} ・・・(5)\]
この式をレイノルズ方程式とよびます。

上式と通常のナビエ・ストークス方程式を比較すると、上式には右辺の最後の項が余分についており、この項がレイノルズ応力を示します。
2. 乱流混合に関する仮設
(1)ブジネスクの渦動粘性係数
式(3)で示した渦によるレイノルズ応力を、通常の粘性せん断応力\(\rho v d \bar{u}/dy\)と同様の形であると仮定すると、
\[-\rho \overline{u’v’}=\rho \epsilon d \bar{u}/dy ・・・(6)\]
動粘性係数\(\nu\)に対して、\(\epsilon\)を渦動粘性係数(kinematic eddy viscos)とよびます。\(epsilon\)は物性値ではなく、流れの状態によって変化します。
(2)プラントルの混合距離
ある点の変動速度は、流体粒子の移動距離間の平均速度勾配に比例すると考えられることから、
\[
\left| u’ \right| \approx \left| v’ \right| \approx \left| \frac{\displaystyle d\bar{u}}{\displaystyle dy} \right| ・・・(7)
\]
したがって、
\[
-\rho \overline{u’v’}=\rho l^2 \left| \frac{\displaystyle d\bar{u}}{\displaystyle dy} \right| \frac{\displaystyle d\bar{u}}{\displaystyle dy} \\
\epsilon = l^2 \left| \frac{\displaystyle d\bar{u}}{\displaystyle dy} \right| ・・・(8)
\]
上式をプラントルの混合距離の仮設(mixing length hypothesis)とよび、\(l\)を混合距離(mixing length)といいます。
壁面に近い乱流の場合、混合距離は壁面に抑えられ\(y\)に比例します。
\[l=ky\]
上式を式(8)に代入すると式を得られます。
\[
-\rho \overline{u’v’}=\rho k^2 y^2 \left| \frac{\displaystyle d\bar{u}}{\displaystyle dy} \right| \frac{\displaystyle d\bar{u}}{\displaystyle dy} ・・・(10)
\]

