流体｜プラントルの壁法則に基づいた対数分布則の導出

　流体に関わる設計者であれば摩擦圧力損失の抑制が課題の一つだと思います。圧力損失をイメージするうえで大切な流れの発達について解説し、CFD解析でよく使われる対数分布則の導出をしたいと思います。

1. 菅の流入部の流れと十分に発達した流れ

　図に示すような大きな空間から一様断面の管路に流れ込む流れの流速分布と圧力損失を取り扱います。

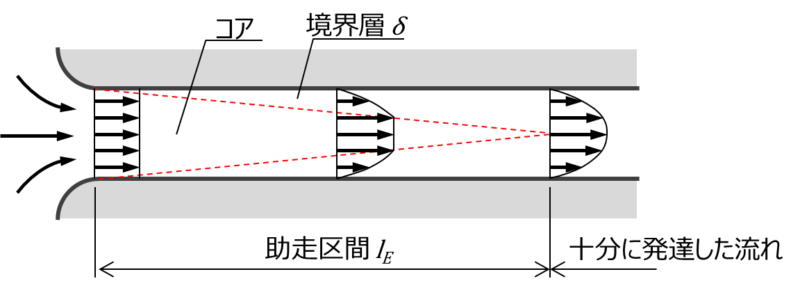
管の入口では、一様な流速分布です。流れが進むと粘性により壁面から境界層が成長します。これにより、流れが絞られるように（質量保存（連続の式））中心部の流速が増します。ここで境界層が十分に発達する管路入口からの距離を\(l_E\)と定義します。壁面からの境界層が層流のままでであれば\(l_E/d=0.065Re\)となります。しかし、ほとんどの実際の流れでは境界層の成長にしたがって局所レイノルズ数Reが限界に達して乱流境界層へと遷移します。

2. 壁法則と速度欠損

　壁面近くの流れは、密度\(\rho\)、動粘性係数\(\nu\)、壁面摩擦応力\(\tau_0\)、壁からの距離\(y\)により決まります。ここで、
\[U_{\tau}=\sqrt{\tau_0/\rho}　　・・・(1)\]
は速度の次元をもちますので速度の物差しとして使えます。これを摩擦速度と呼びます。これらを用いて無次元長さを
\[\eta=\frac{\displaystyle U_{\tau}y}{\displaystyle \nu}　　・・・(2)\]
で定義すれば、壁面近くの速度分布は
\[ \frac{\displaystyle \overline{u}(y)}{\displaystyle U_{\tau}} =f_n\left(\frac{\displaystyle U_{\tau}y}{\displaystyle\nu}\right)　　・・・(3)\]
の形にできます。レイノルズ数に無関係になっており、これをプラントルの壁法則といいます。

　上記に対して、管の中央部での流れは、管壁での摩擦応力と切り離して考えることができ、流れの場の全体的な量（\(a(=d/2)\)、\(U_{max}\)もしくは\(\tau_0\)、\(\rho\)）によります。これらより次の流速分布（無次元）が成り立ちます。
\[ \frac{\displaystyle U_{max}-\overline{u}(y)}{\displaystyle U_{\tau}} = f_n \left(\frac{\displaystyle y}{\displaystyle a}\right)　　・・・(4)\]
これはカルマンの速度欠損則と呼ばれています。

3. 混合距離と流速分布

　ここでは、壁法則としてよく使われる以下の対数速度則を導出したいと思います。

　十分に発達した管路の乱流を考えます（流れの方向に一様）。2次元で考えるために、円形の管路を考えます。平均流速\(u(y)\)に関するレイノルズの方程式（流体の運動方程式）の左辺の項は全部０となります。（以降、\(\overline{u}\)を\(u(y)\)や単に\(u\)と記載します）
レイノルズの方程式
\[\frac{\displaystyle \partial u}{\displaystyle \partial t}+u\frac{\displaystyle \partial u}{\displaystyle \partial x}+v\frac{\displaystyle \partial u}{\displaystyle \partial y}=
-\frac{\displaystyle 1}{\displaystyle \rho}\frac{\displaystyle \partial p}{\displaystyle \partial x}+\frac{\displaystyle 1}{\displaystyle \rho} \left( \frac{\displaystyle \partial \tau_{xx}}{\displaystyle \partial x}+\frac{\displaystyle \partial \tau_{xy}}{\displaystyle \partial y} \right) 　　・・・(5)\]
これが次の様になります。
\[ 0= -\frac{\displaystyle 1}{\displaystyle \rho}\frac{\displaystyle \partial p}{\displaystyle \partial x}+\frac{\displaystyle 1}{\displaystyle \rho}\frac{\displaystyle \partial \tau_{xy}}{\displaystyle \partial y} 　　・・・(6)\]
したがって、\(-(\partial p/\partial x)+(\partial \tau/\partial y)=0\)となり、これを積分して次の式になります。
\[\tau=\frac{\displaystyle (a-y)}{\displaystyle 2}\left( -\frac{\displaystyle \mathrm{d} p}{\displaystyle \mathrm{d} x}\right) 　　・・・(7)\]
ここで\(a\)は円管の半径です。粘性応力とレイノルズ応力（乱流による応力）の和が剪断応力\(\tau\)となります。壁面のごく近傍を除けば粘性は作用せずに剪断応力はほとんどレイノルズ応力で決まります。これを式で表すと次の様になります。
\[\begin{eqnarray}
\tau&=& \mu\frac{\displaystyle \partial u}{\displaystyle \partial y}-\rho \overline{u’v’} \\
&≒& -\rho \overline{u’v’}
\end{eqnarray}　　・・・(8)\]
ここで、プラントルの混合距離理論を用いると次のように表現できます。
\[ \tau=\rho l^2 \left|\frac{\displaystyle \mathrm{d}u}{\displaystyle \mathrm{d}y} \right| \frac{\displaystyle \mathrm{d}u}{\displaystyle \mathrm{d}y}　　・・・(9)\]
混合距離\(l\)に関して次の様に仮定します。
\[l=\kappa y　　・・・(10)\]

レイノルズ応力および乱流混合｜乱流の基礎から方程式の導出

乱流の定義と物理的な意味をレイノルズの実験による成り立ちからわかりやすく解説します。

vis-tech.site

管路乱流の剪断応力は直線分布（レイノルズ応力を積分してられた式：\(y\)の関数）となります。しかし、上記のプラントルの仮定では剪断応力\(\tau\)と壁面剪断応力\(\tau_0\)は等しくなります。剪断応力分布は次のようになります。
\begin{eqnarray} \tau=\tau_0 \begin{cases}
=-\frac{\displaystyle \mathrm{d} p}{\displaystyle \mathrm{d} x}\cdot a&(二次元管路)\\
=-\frac{\displaystyle \mathrm{d} p}{\displaystyle \mathrm{d} x}\cdot \frac{\displaystyle a}{\displaystyle 2}&(円管路)
\end{cases}　　・・・(11)\end{eqnarray}

プラントルの混合距離理論の式に上式の\(\tau\)および\(l\)の関係式を代入すると管内の流速が求められます。（\(\tau = \tau_0=const.\)とします）また、\(\mathrm{d} u/\mathrm{d} y\)がこの場合は常に正の値になることから絶対値記号は不要となり次の式が得られます。（絶対値記号は２乗の形になって方向性が消えるのを避けるためのテクニックです）
\[ \frac{\displaystyle \tau_0}{\displaystyle \rho}=(\kappa y)^2 \left( \frac{\displaystyle \mathrm{d} u}{\displaystyle \mathrm{d} y} \right)^2 　　・・・(12)\]
上式を変形すると
\[ \frac{\displaystyle \mathrm{d} u}{\displaystyle \mathrm{d} y} = \frac{\displaystyle U_{\tau}}{\displaystyle \kappa y} 　　・・・(13)\]
ここに摩擦速度\(U_{\tau}=\sqrt{\tau_0/\rho}\)を上式に代入して積分すると
\[\frac{\displaystyle u(y)}{\displaystyle U_{\tau}}= \frac{\displaystyle 1}{\displaystyle \kappa}ln y +C_1　　・・・(14)\]
ここで、プラントルの壁法則；流速分布は\(\rho\)、\(\nu\)、\(\tau_0(U_{\tau})\)、\(y\)により支配されることを考えます。すると、支配量（\(\nu\)、\(U_{\tau}\)、\(y\)）で作られる無次元長さに置き換え、新たに普遍定数\(A_s\)（sはsmooth）を導入して次の様に書くことができます。
\[\frac{\displaystyle u(y)}{\displaystyle U_{\tau}}= \frac{\displaystyle 1}{\displaystyle \kappa}ln \frac{\displaystyle U_{\tau}y}{\displaystyle \nu} +A_s　　・・・(15)\]
これを対数分布則と言います。

CFDをかじったことがある方はこの対数分布則を見たことがあると思います。今回はこの対数分布則の導出までを一旦ゴールとし、実際の粘性低層に対する理解や圧力損失につながる摩擦抵抗については、次回以降で解説したいと思います。